从图3同样可以看出,长方形玻璃板,随着孔心边距的增大,玻璃板中心和板边中心的位移也呈现迅速下降的趋势。为了控制玻璃板的变形,同时也需要考虑孔心边距对孔边缘集中应力的影响,我们研究发现,比较合理的孔心边距是100mm。
(3)正方形玻璃板变形随玻璃厚度的变化(见图4孔心边距为100~),其边长分别为2、1.8、1.5、1.2舫擒厚詹为6、8、10、12、15mm。
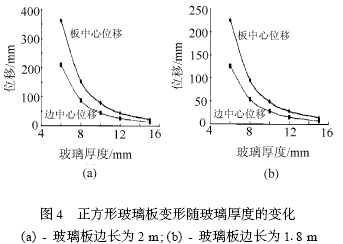
从图4中可以看出,正方形玻璃板,随着玻璃板厚度的增大,玻璃板中心和板边中心的位移也呈现迅速下降的趋势。
(4)长方形玻璃板变形随玻璃厚度的变化(见图5)孔心边距为l00 mm,计算模型共4组,其边长分别为2mXl.8m、2m Xl.5m、2mXl.2m、2 m X1m破璃厚度为6、8、10、12、15mm。考虑孔的影响,孔径为36mm。
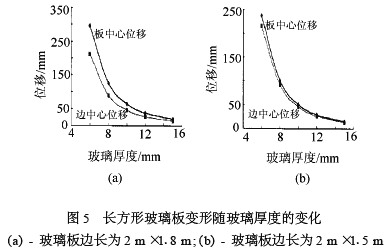
从图5同样可以看出,长方形玻璃板,随着玻璃板厚度的增大,玻璃板中心和板边中心的位移也呈现迅速下降的趋势。
通过以上计算可以看出:
(1)对于目前通用的长方形和正方形玻璃板,随着支承点孔心边距的增大玻璃板中心和玻璃板板边中心的位移减小。这主要是因为孔心边距的不断增大,外围玻璃板受力的反翘作用使得玻璃板中心和玻璃板边缘处的应力减少位移得到控制。
(2)当玻璃板的尺寸和玻璃孔心边距相同时,随着玻璃厚度的增大玻璃板中心和边缘中心处的位移不断减小。这是因为厚度的增加便得玻璃板抵抗垂直于平面的
弯曲能力加强,从而玻璃板边缘和中心的位移变小。
4、点式连接玻璃板变形性能的试验结果比较分析
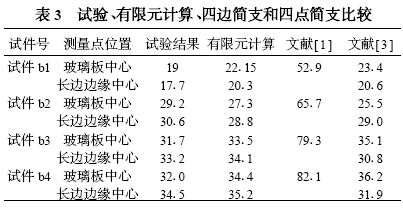
为研究点式玻璃的承载性能我们进行了1:1模型加载试验t9,将试件按bl、b2、b3、b4编号。试验模型采用实际工程的同批试件尺寸为1.260m X0.890m-1.36m X0.9m荷载为均布考虑孔的影响孔径为36 mm,厚度为12mm。为了便于比较我们按试件具体尺寸进行相应的有限元计算表3中还列出文献[1]和文献[3]计算公式的计算结果。
 上一页1234下一页
上一页1234下一页
