目前很多的门窗公司在计算隔热铝合金门窗抗风压性能方面,缺少理论计算方法的支持,因此,显得办法不多,很是无奈;于是“旁引”了一些不科学的计算公式进行计算,结果有两种可能:一种是中梃杆件的“钢度”不稳定,因此而造成了工程质量的隐患,导致门窗的气密性差,保温性能下降,遇见风雨交加的天气时候门窗漏水;另一种是中梃杆件的“钢度”设计安全系数过大,造成不必要的浪费。
美国建筑制造协会(AAMA)TIR-A8-04标准,就隔热梁的挠度计算、最大压缩和拉伸应力计算、最大纵向剪切应力计算描述的很清楚,是门窗设计师的参考书。
一计算原理:
1、隔热梁的挠度和等效惯性矩计算:
本文是对于一个具有非均一截面的简支梁在集中或均布载荷作用下,预算其等效惯性矩的方法。这个模型是由相对硬面(如铝合金)与较软的核心材料(隔热聚氨酯结构胶)持续联结在一起的“复合”梁。
计算隔热铝合金型材的关键问题是隔热材料的剪切形变。在计算纯铝合金型材的简支梁受到集中或均布载荷时,其公式为:伯努利-欧拉方程(EIy"=M) ,而将其剪切变形量忽略不计。然而,当型材轴向上的立筋存在相对较软的隔热材料时,会导致“复合”梁的行为复杂化。受到载荷时,“复合”梁的横截面尺寸会因隔热材料的剪切形变而产生变化。隔热材料的剪切形变使得其形状由矩型变成平行四边型。
由于隔热材料位于两块铝合金型材之间,当其作为简支梁承受力的作用时,整个复合型材的变形量以及铝合金型材所受到的应力较纯铝合金型材都有所增加;相反在长度方向上所传递的剪切流(隔热胶的剪切应力乘以隔热胶的宽度b’)却减弱了很多。
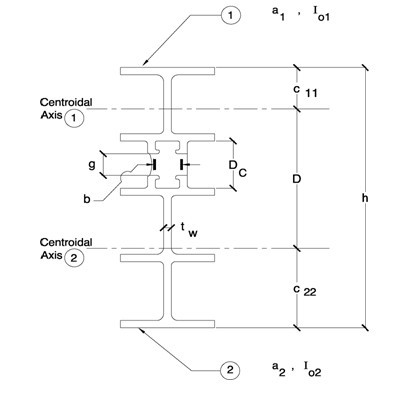
图一
在公式和图示中我们将用到以下参数:
A= tw (h-g) —铝合金材料的剪切面积 (mm2)
AC — 弹性体的总截面积 (mm2)
a1,a2 —铝型材表面1和2的面积 (mm2)
b=AC/DC —弹性体的平均宽度 (mm)
b’ —两个凸点间的净宽度 (mm)
c11,c22,D —分别是形心轴线到两个铝合金型材外表面的距离,以及两形心轴线间的距离。(mm)
DC —断热槽的最大深度 (mm)
E=70000N/mm2 —铝型材的杨氏模量
EC—弹性体的杨氏模量 (1650 N/mm2)
g —隔热槽两个凸点的隔热距离 (mm)
GC= EC/[2(1+v)] —弹性体的剪切模量 (N/mm2) ;v是弹性体的泊松比(Poisson’s ratio)
h—铝型材截面的总宽度 (mm)
h1,h2—铝型材的重心到两个外表面的距离 (mm)
I02—铝型材1和2的惯性矩 (mm4)
L—跨度,两个支点间的距离 (mm)
W0—均布载荷 (N/mm)
P—集中载荷 (N)
tw —铝型材轴向立筋的厚度,或厚度的总和。tw = Aw /(h-g), Aw 是两块型材各个立筋乘以其相应高度之和。
参数、综合恒量和基本公式
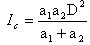 该值仅适用于复合型材的两段均为同一材料的情况下 (mm4) 该值仅适用于复合型材的两段均为同一材料的情况下 (mm4)
••••(1)
I0=I01+I02是等效惯性矩的较低值。(铝型材内表面和胶接触的表面上,有相对滑动的情况) (mm4)
•••••••••••••••• (2)
I=IC+I0 是等效惯性矩的较高值。该值仅在铝型材内表面和断热胶接触的表面没有任何剪切变形时 (mm4)
•••••••••••••••••••••••••••••(3)
IC/I •••••••••••••••••••••••••••••••••••••••••(4)
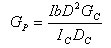 (N) ••••••••••••••••••••••••(5) (N) ••••••••••••••••••••••••(5)
 仅对于两面的材质具有相同的E值 (1/mm2) ••••••••••(6) 仅对于两面的材质具有相同的E值 (1/mm2) ••••••••••(6)
因为隔热铝合金型材杆件的理论惯性矩Ie 是L(跨矩)、GC(隔热胶的剪切模量)和载荷形式(如:集中载荷或均布载荷)的函数,它不同于普通铝合金型材的惯性矩(是与截面有关的常数)。所以,首先要计算出在集中载荷或均布载荷作用下的复合杆件形变,再计算其相应的理论惯性矩Ie。的值。
对于“复合”梁的弯曲力矩(M)和剪切力(V),相关于发生弯曲形变(y),其相关的微分公式为:
 (1/mm3) ••••••••••••••••••••••••••(7) (1/mm3) ••••••••••••••••••••••••••(7)
公式中的(´)表示对x的微分。
当集中载荷时,其弯矩方程为:
 •••••••••••••••••(8) •••••••••••••••••(8)
将公式(8)代入公式(7),整理后得(隔热铝合金梁在集中载荷时的形变曲线方程):
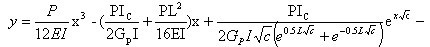
 •••••••••••••(9) •••••••••••••(9)
公式中的 为自然对数的底。
当均布载荷时,其弯矩方程为:
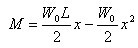 •••••••••••••••(10) •••••••••••••••(10)
将公式(10)代入公式(7),整理后得(隔热铝合金梁在均布置载荷时的形变曲线方程):
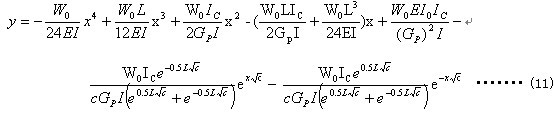
以下为等效惯性矩的计算公式,该公式未考虑剪切变形的影响。
注意:y=最大弯曲形变
集中载荷: Ie = PL3 / 48Ey ••••••••••••••••••••••••••••••••••• (12)
均布载荷: Ie=wL4/ 76.8Ey = (wL)L3/ 76.8Ey ••••••••••••••••••(13)
注意:因为y是许多变量的函数。因此,惯性矩Ie也是。特别要指出的是,Ie 是L(跨矩),GC(弹性体的剪切模量)和载荷形式(如:集中载荷或均布载荷)的函数。
如果F(形状因素)近似为1(对于“I”梁可以适用),则隔热型材的等效惯性矩的计算公式如下:
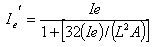 •••••••••••••••••••(14) •••••••••••••••••••(14)
均布载荷: 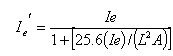 •••••••••••••••••(15) •••••••••••••••••(15)
2隔热梁的最大压缩应力和拉伸应力计算:
在复合铝合金型材任意截面内,上半部型材的平均压缩力(F1)与截面内不同的压缩力之和相等;F1的作用点为上半部型材的形心(在上半部型材的中心轴线上)。下半部型材的平均拉社伸力(F2)与截面内不同的拉伸力之和相等;F2的作用点为下半部型材的形心(在下半部型材的中心轴线上)。由于隔热材料与铝合金的弹性模量想差悬殊,故隔热材料的压缩、拉伸应力忽略不计。
由于隔热胶的剪切形变,任意截面内(延着中心轴线)存在着一个平均压缩力(F1)和一个平均拉伸力(F2)。因复合型材杆件的静止,所以,两力相等(F1=F2),方向相反。
任意截面内(延着中心轴线),上半部型材的中心轴线之上,压缩应力增加;上半部型材的中心轴线之下,压缩应力减少,应力间相互平衡。同样的情况,下半部型材的中心轴线之上,拉伸应力减少;下半部型材的中心轴线之下,压缩应力增加,应力间相互平衡。
M = Mc + Mo ••••••••••••(16)
M :由于受到均布载荷,而在中梃杆件截面内产生的力矩。
Mc :由于两个大小相等、方向相反的平均力(F1、F2),而产生的力矩。
Mo :由于两块铝合金型材截面内应力分布的不同,而产生的力矩。
中梃的上面(室外侧)型材质心受到的平均压缩应力为: -(M-EI0y’’)/ a1D;••••••••••(17)
中梃的下面(室内侧)型材质心受到的平均拉伸应力为: (M–EI0y’’)/ a2D;••••••••••(18)
中梃的上面(室外侧)型材受到的最大压缩应力存在于型材的最外侧,故:
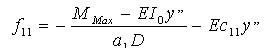 ••••••••••••••••••(19) ••••••••••••••••••(19)
中梃的下面(室内侧)型材受到的最大拉伸应力存在于型材的最内侧,故:
 •••••••••••••••••••(20) •••••••••••••••••••(20)
3隔热梁的最大纵向剪切应力计算:
作用在中梃杆件任意截面上的剪切力V是由铝合金型材和隔热胶共同承担的,此时铝合金型材的受到的力矩为:Mal = EI0(dy2/dx2) ;
而铝合金型材受到的剪切力V可表示为:Val = dMal /dx = EI0(dy3/dx3) ••••••••(21)
那末,隔热胶受到的剪切力为:Vsc = V - EI0(dy3/dx3) •••••••••••••• (22)
隔热胶受到的剪切应力为:Ssc = (V - EI0(dy3/dx3) )÷(bD) •••••••••••••(23)
在注胶隔热铝合金型材中任取一块长度为dx的聚氨酯立方体,因其静止,故:
1合外力等于零。上、下两边的剪切力大小相等,方向相反。同理,左右、前后两边的剪切力也大小相等,方向相反。
2相对于任意点的力矩等于零。可以得出:这六个力的大小相等;垂直于隔热铝合金型材杠件的任意面,其剪切应力与纵向剪切应力(N/mm2)相等。
那末,隔热铝合金型材的纵向剪切力为:T = Ssc×b’ ••••••••••••••••(24)
 [本文共有 2 页,当前是第 1 页] [本文共有 2 页,当前是第 1 页]  [1] [2] [1] [2] 
|