本篇文章内容由[中国幕墙网ALwindoor.com]编辑部整理发布:
在幕墙立柱设计当中,《上海市建筑幕墙工程技术规程》DGJ08-56-2012[1] 第12.5.1条表明“应根据立柱的实际受力和支承条件,分别按单跨梁、双跨梁或多跨梁计算由自重、风荷载和地震作用产生的弯矩(词条“弯矩”由行业大百科提供)、扭矩和剪力(词条“剪力”由行业大百科提供),并按其支承条件计算轴向力(词条“轴向力”由行业大百科提供)”,即幕墙立柱设计是由主体结构、地理环境和自身构造决定的。在大跨度层高(≥4500mm)、大载荷情况下,立柱上端常采用双支座形式,分为长短两跨以满足结构要求,计算模型是按照双跨梁。此模型对真实构造的简化处理,主要集中在顶部和中部的支座螺栓和底部立柱插接套芯部分,双跨梁将复杂的梁与支座面接触关系简化成单纯铰接作用。
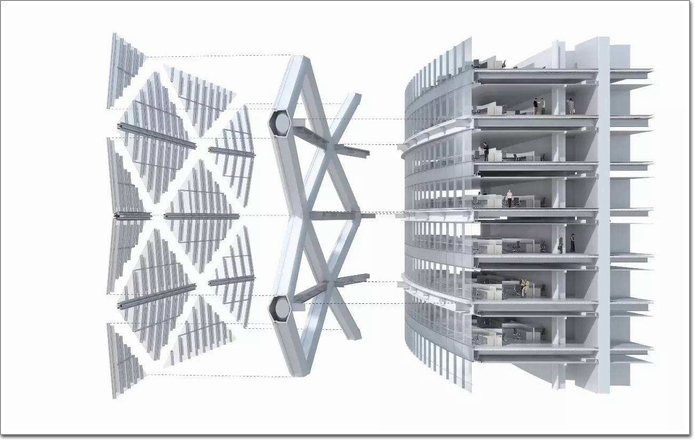
目前,贵州大学土木学院对双跨梁支座约束机理有一些初步结果,特别是对于立柱—插芯之间的连接构造对计算模型的影响问题做了分析探讨,得出立柱—插芯连接处属于半刚性或接近全刚性的结论[2]。但目前对双支座螺栓的固定连接还未有明确的研究结果,也就无法了解该部位的真实作用状态和机理,及其对整理立柱响应的贡献,为此文中进行了这方面研究的拓展和补充。
《铝合金结构设计规范》GB 50429-2007[3]第4.2.4条指出“框架结构(词条“框架结构”由行业大百科提供)内力分析可采用一阶弹性分析”。在考虑对比不同算法之前有必要明确理论和有限元方法的前提假设。简而言之,理论计算涉及到材料力学基本假设,即平截面(词条“截面”由行业大百科提供)(几何线性)、胡克定律(材料线性)和边界不变性(边界线性),整体刚度(词条“刚度”由行业大百科提供)保持不变;此次有限元分析是按线性、弹性的(几何与材料线性)和支座接触(边界非线性)来模拟,整体刚度将由于接触关系而变化。

1 双跨梁理论模型
作为对立柱双跨梁横向作用效应(词条“作用效应”由行业大百科提供)的比较,风荷载和地震作用比自重更具有问题相关性。因此纵向的立柱及附属构件的自重荷载,作为理论分析暂不考虑。同时为了研究的针对性,模型对比均不考虑立柱构件的局部和整体稳定计算。
1.1. 总体信息
某工程位于广州市 (7度设防,设计地震基本加速度0.10 g),地面粗糙度C类,建筑高60m,层间高度为4.5 m,结构梁高650 mm,框架式幕墙, 8+12A+8 mm中空玻璃分格(B×H)1.0×1.5 m,预埋件侧埋,立柱采用双支座,受结构梁高度限制,立柱短跨为500 mm,长跨4000 mm,如组图 1
基本风压:0.5 kPa;
风荷载标准值(词条“标准值”由行业大百科提供):Wk=1.7 kPa;(墙角区)
玻璃幕墙构件自重:g=0.5 kPa;
地震作用:qEH=5×0.08×0.5=0.2 kPa;
荷载标准值:w=1.7 + 0.5×0.2 = 1.8 kPa
荷载设计值:W=1.4×1×1.7 + 1.3×0.5×0.2 = 2.51 kPa;
幕墙立柱跨度:L=4.5 m,短跨 L1=0.5 m,长跨 L2=4 m,短跨比 b=1/9;
立柱材性:铝合金型材(词条“铝合金型材”由行业大百科提供)6063-T6,E=70000 Mpa;
立柱截面:惯性矩I=1992814 m4,抵抗矩 W=31533 mm3,净距 S=1992800 mm3。
1.2. 理论计算

(a)双支座立柱模型
1.2.1. 荷载

(b)荷载分布
1.2.2. 弯矩图(kN.m)
荷载设计组合2.51kN/m

(c)立柱弯矩
1.2.3. 剪力图(kN)
荷载设计组合2.51kN/m

(d)立柱剪力
1.2.4. 挠度
荷载标准组合1.8kN/m

(e)立柱挠度
1.3. 单元验算
图中数值自上而下分别表示:最大剪应力与设计强度比值;最大正应力与设计强度比值;最大稳定应力与设计比值

(f)立柱强度验算比
图1 某工程案例立柱双跨梁理论计算(a)~(f)
1.3.1. 内力范围、最大挠度
(a)、内力范围:弯矩设计值 -3.02~4.47 kN.m
剪力设计值 -3.90~6.14 kN
(b)、最大挠度:最大挠度20.5mm,最大挠跨比1/195
(挠度允许值《铝合金结构设计规范》(GB 50429-2007) Tab 4.4.1 按1/180)
1.3.2. 强度应力
最大剪应力 τ = Vmax × S / I / tw
= 6.14 × 19277 / 1992800 / 5.0 × 1000
= 11.9 MPa ≤ fv = 85 MPa 满足!
上边缘最大正应力 σ上 = Mmax / γ上 / W上= 4.47 / 1.05 / 31533 × 1e6 = 135.0 MPa ≤ f = 150 MPa 满足!
下边缘最大正应力 σ下 = Mmax / γ下 / W下= 4.47 / 1.05 / 31533 × 1e6
= 135.0 MPa ≤ f = 150 MPa 满足!
连续梁验算结论: 满 足 !
1.3.3. 稳定应力
整体稳定系数φb = 1.00
最大压应力 σ = Mmax / φb / W
= 4.47 / 1.00 / 31533 × 1e6
= 141.8 MPa ≤ f = 150 MPa 满足!
该跨验算结论:满足!
2 简支梁理论模型
从图1(e)双跨梁长短跨挠度对比发现,其挠度响应主要都表现在长跨段,短跨在双支座约束下挠度基本可以忽略。因此作为补充对比模型I,拟取长跨段作为分析对象按简支梁进行理论计算。
2.1. 理论计算

(a)长跨段简支梁理论模型
2.1.1. 荷载

(b)荷载分布
2.1.2. 弯矩图(kN.m)
荷载设计组合2.51kN/m

(c)立柱弯矩
2.1.3. 剪力图(kN)
荷载设计组合2.51kN/m

(d)立柱剪力
2.1.4. 挠度
荷载标准组合1.8kN/m
11

(e)立柱挠度
图2 简支梁I理论计算(a)~(e)
2.2. 强度应力
鉴于此模型仅作为对比项,不作具体验算。
2.2.1. 内力范围、最大挠度
(a)、内力范围:弯矩设计值 -5.02~0.00 kN.m
剪力设计值 -5.02~5.02 kN
(b)、最大挠度:最大挠度43.01mm,最大挠跨比1/93
2.2.2. 强度应力
最大剪应力 τ = Vmax × S / I / tw
= 5.02 × 19277 / 1992800 / 5.0 × 1000
= 9.7 MPa
上边缘最大正应力 σ上 = Mmax / γ上 / W上
= 5.02 / 1.05 / 31533 × 1e6
= 151.6 MPa
下边缘最大正应力 σ下 = Mmax / γ下 / W下
= 5.02 / 1.05 / 31533 × 1e6
= 151.6 MPa
2.2.3. 稳定应力
整体稳定系数φb = 1.00
最大压应力 σ = Mmax / φb / W
= 5.02 / 1.00 / 31533 × 1e6
= 159.1 MPa
3 一端固支一端简支理论模型
作为补充对比模型Ⅱ,取长跨段作为分析对象,将短跨缩减为固接端进行理论计算。
3.1. 理论计算

(a)长跨段理论模型
3.1.1. 荷载

(b)荷载分布
3.1.2. 弯矩图(kN.m)
荷载设计组合2.51kN/m

(c)立柱弯矩
3.1.3. 剪力图(kN)
荷载设计组合2.51kN/m

(d)立柱剪力
3.1.4. 挠度
荷载标准组合1.8kN/m

(e)立柱挠度
图3 双跨梁长跨段一端固支一端简支Ⅱ理论计算(a)~(e)
3.2. 强度应力
鉴于此模型仅作为对比项,不作具体验算。
3.2.1. 内力范围、最大挠度
(a)、内力范围:弯矩设计值 -2.79~5.02 kN.m
剪力设计值 -3.76~6.27 kN
(b)、最大挠度:最大挠度17.89mm,最大挠跨比1/224
3.2.2. 强度应力
最大剪应力 τ = Vmax × S / I / tw
= 6.27 × 19277 / 1992800 / 5.0 × 1000
= 12.1 MPa
上边缘最大正应力 σ上 = Mmax / γ上 / W上
= 5.02 / 1.05 / 31533 × 1e6
= 151.6 MPa
下边缘最大正应力 σ下 = Mmax / γ下 / W下
= 5.02 / 1.05 / 31533 × 1e6
= 151.6 MPa
3.2.3. 稳定应力
整体稳定系数φb = 1.00
最大压应力 σ = Mmax / φb / W
= 5.02 / 1.00 / 31533 × 1e6
= 159.1 MPa
4 有限元模型
4.1. 仿真分析
结构有限元分析软件采用solidThinking Inspire,拥有Altair先进的OptiStruct优化求解器,在一个友好易用的软件环境中提供“仿真和驱动设计”的创新工具。根据给定的设计空间、材料属性以及受力需求,Inspire可以自动进行自适应网格划分和计算,简化了单元划分和边界设置,减少整个分析流程的时间。

图4 双跨梁立柱支座节点
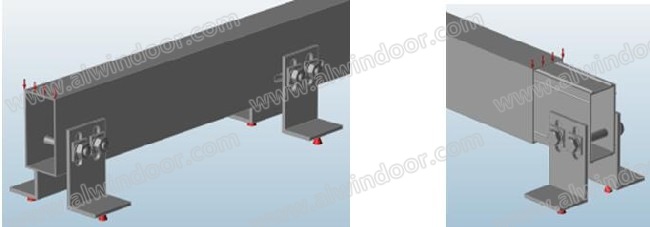
图5 支座螺栓与底部套芯
根据该幕墙工程立柱支座节点,如图4,其特征是,支座采用了2xM12不锈钢A4-70螺栓由双角钢夹持同立柱连接,底部采用的250mm长铝型材套芯将上下立柱插接;螺栓间距40mm,带30x4mm钢垫片,角钢和立柱中支座处开长圆孔。为反映上述典型构造,研究必须建立在构件实体及其配合关系上。因此如图5,有限元模型按照设计构造尺寸定义了型材、支座螺栓、圆孔、长孔和角钢垫片,在套芯处同样设置了螺栓支座以作固定;考虑研究目标是螺栓和套芯与立柱的约束关系,在此将垫片与角钢作为整体,重点处理螺杆(词条“螺杆”由行业大百科提供)与立柱孔壁的承压接触以及套芯肋线与立柱内壁挤压接触设置。
经过等效加载,将计算横向线荷载标准值转换为有限元立柱表面荷载,获得图6~7 变形和应力结果。可知跨中最大位移14.3mm,中支座附近立柱上下边缘最大拉压应力标准值90.6Mpa/-86.7Mpa,设计值为126.3Mpa/-120.8Mpa。较小于理论模型的最大挠度20.5mm(差异25.9%),最大中支座应力±141.8Mpa(差异14.8%);有限元分析整体呈现出比双跨简支梁更好的刚度。局部来看,透过图8发现同一支座的两颗螺栓处在不同的拉压区域,呈现一对力偶的形态,抵抗中支座最大弯曲(词条“弯曲”由行业大百科提供)内力,造成该长圆孔局部螺栓接触应力达到最大的244.6Mpa,超过了立柱型材6063一T6的屈服强度150Mpa;同样支座套芯的应力云图9观察到其顶面应力分布呈现出前后明显的拉压分区,表明套芯在约束着立柱的相对转动,并且最大应力达到220Mpa,也出现了局部的屈服。
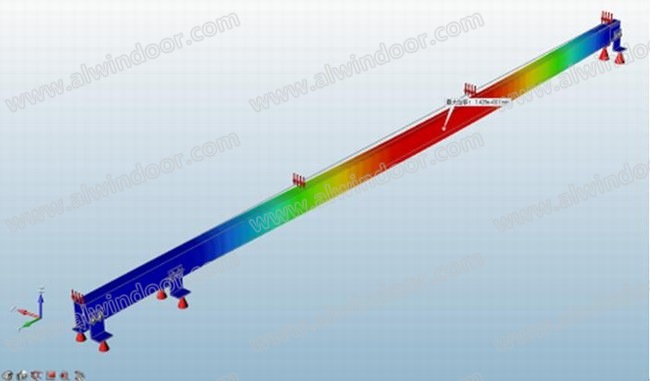
图6 最大挠度14.29mm
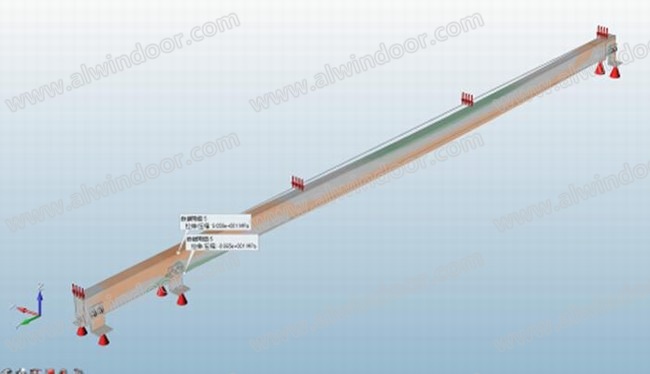
图7 最大拉压应力标准值90.6Mpa/-86.7Mpa
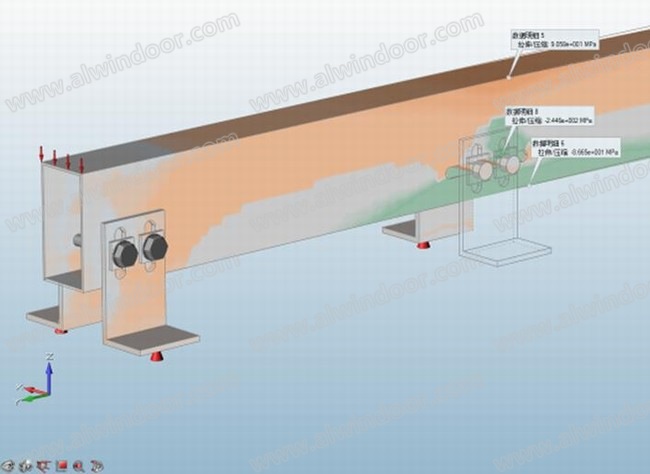
图8 支座螺栓应力区域分布
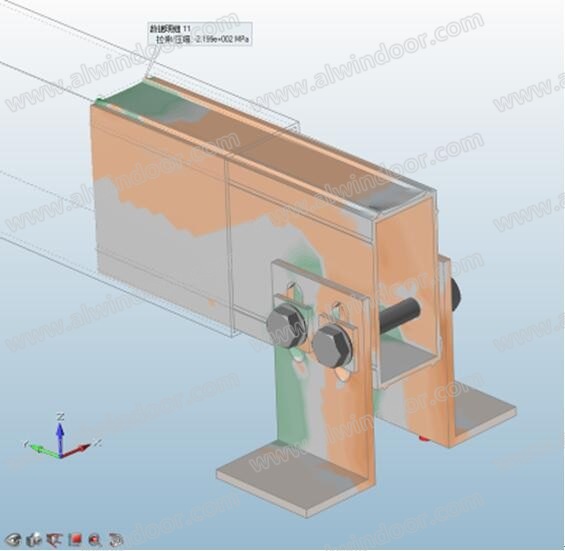
图9 套芯应力区域分布
4.2. 结果对比
通过有限元结果,验证了真实支座抗弯刚度的特性,为进一步了解立柱双支座转动刚度的大小,此处再以分析所得数据,即双跨梁、长跨段简支梁模型(I)、长跨段一端固支一端简支梁模型(Ⅱ)和双跨梁有限元模型来分别与双跨梁模型对比界定,如表1所示。
表1 双跨梁计算分析结果对比

结果显示,按惯用理论计算相比有限元分析更为保守(挠度和应力)。以支座铰接模型I的计算结果,挠度相比双跨梁误差大101%,显然是由于短跨对长跨约束的贡献,将梁抗弯刚度提高了一倍;取模型Ⅱ计算,变形差异为12.7%,应力误差在12.2%水平,介于双跨梁和有限元之间,但更趋近于双跨梁的理论结果,说明了固定端的约束要比短跨稍微更强一些;而实际双螺栓支座是带有一定转动刚度的,若考虑长圆孔对螺栓的转动约束,短跨支座可接近完全刚接的约束极限;再通过模型Ⅱ和有限元比较,发现套芯也有很强的转动刚度,甚至接近于半固端。因此通过有限元模拟和对比分析,解释了双跨梁真实的约束边界,为工程设计师提供了理论参考。
5 结论
针对幕墙中的双支座立柱形态,进行了惯常理论计算与有限元模拟分析,对比了挠度和应力,结果差异相对较大,原因是实际双螺栓支座具有一定的转动刚度,在立柱连接点形成抵抗力偶,而不像铰接点一样自由转动,使得短跨支座趋于固端;另外立柱插芯连接方式具有很强的转动刚性,套芯与立柱内壁紧密挤压,抵抗撬动,能限制一定的立柱变形,近似于半固接点。
[1] DGJ08-56-2012《上海市建筑幕墙工程技术规程》[S]
[2]李绍朗,肖建春,封建波,王泽曦,杜玉涛,吴夏燕.幕墙立柱连接处的接触力学分析[J].贵州大学学报(自然科学版),2016,33(01):117-121.
[3] GB50429-2007《铝合金结构设计规范》[S]

