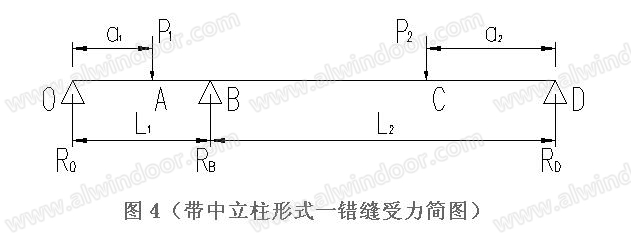
此时单元上横梁受力模型变成超静定体系,受力分析较复杂,以下根据《机械设计手册》中双跨梁受力公式(图5、图6、图7、图8)及按同等条件下的几组有限元模型计算结果进行对比印证。
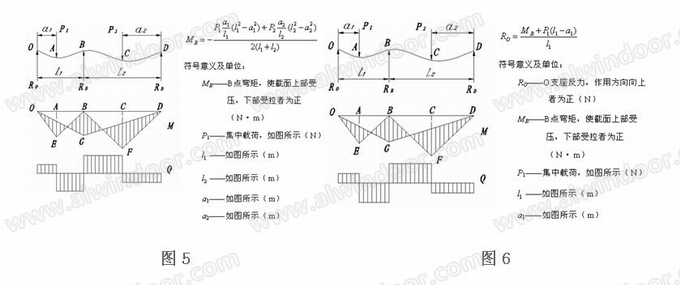
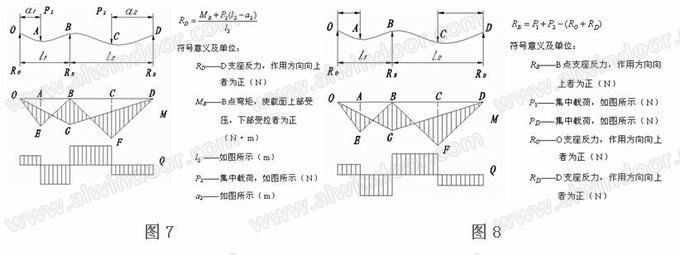
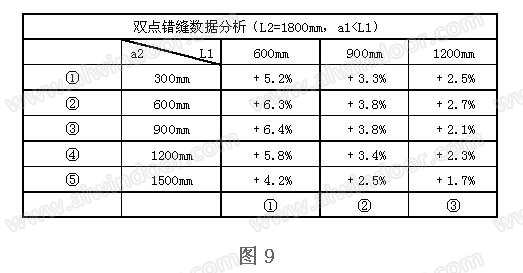
根据几组计算数据分析(图9),简化公式计算值比有限元模型反力值偏大+1.7%~+6.4%左右,两者偏差较小,可以认为两者计算的上横梁连接反力是可相互印证的,设计过程中可按计算出的节点反力对连接节点O、节点B、节点D位置采取不同的连接措施。
2.3 带中立柱形式二错缝分析
板块错缝样式(图10),单元板块A、板块B的单元阴阳料及中立柱两者通过水槽料分别插接在标准下单元板块C、板块D、板块E的上横梁上,上单元的插接受力点落在下单元上横梁位置(形式二),板块传力清晰,对力学模型进行简化分析如下。

带中立柱形式二错缝上横梁受力简图(图11),荷载作用点距支座距离可变,且a1>L1;
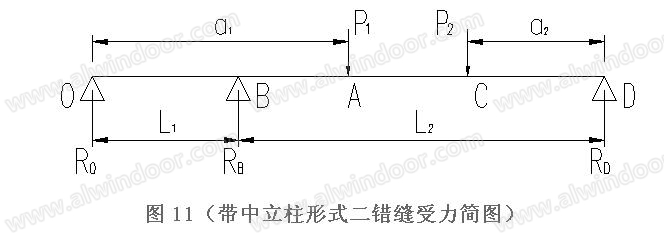
单元上横梁受力模型也是超静定体系,根据《机械设计手册》中双跨梁受力公式计算出的反力结果,与同等条件下的几组有限元模型计算结果对比印证(图12)发现,两者计算结果偏差较大,可知当a1>L1后,不能直接套用公式。
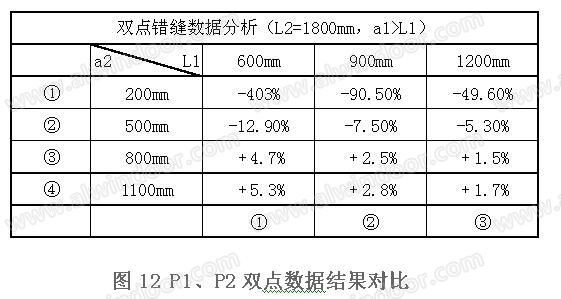
此时我们可以根据叠加原理将形式二错缝受力简图拆分计算(图13),将P1、P2分别进行计算并叠加求出双跨梁连接位置反力,并与同等条件下有限元模型结果进行对比验证,如下分析:
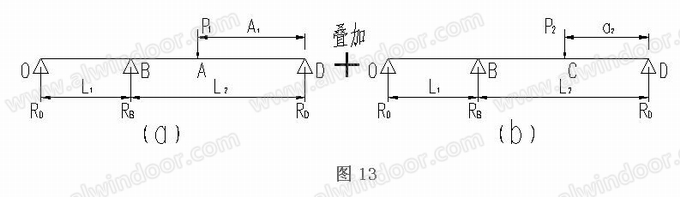
据图5、图6、图7、图8中公式,令其中一个荷载自变量为0,可对公式进行简化,
对图13中(a)有:


分别与同等条件下的有限元模型计算结果对比印证,简化后(图14、图15)及叠加后(图16)。
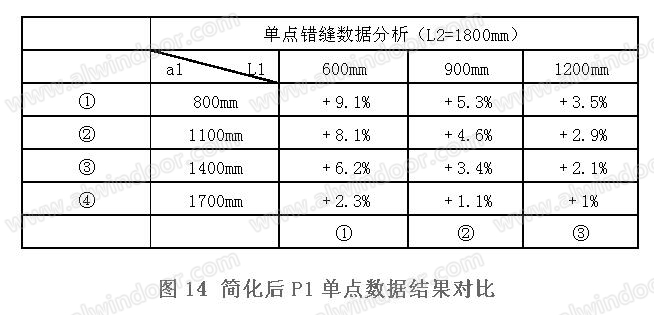
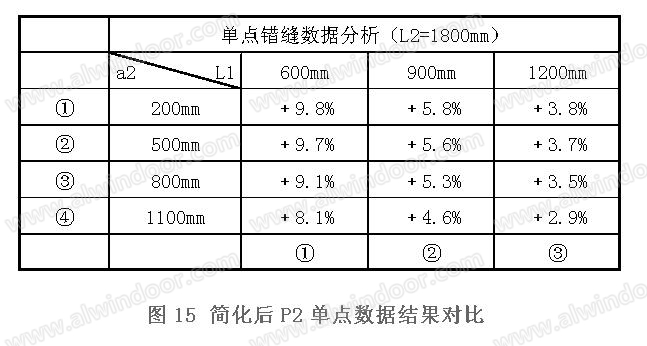
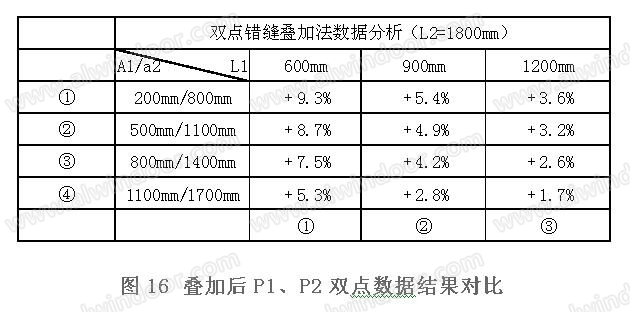
经过计算数据对比,发现简化公式计算值相较于有限元模型反力值偏大+1.7%~+9.3%左右,两者偏差较小,设计过程中可按叠加法公式①、②、③、④计算出形式二错缝的节点反力,并对连接位置采取不同的连接措施。
3、错缝式单元幕墙横梁连接受力不均匀性方案选择
错缝式单元幕墙荷载受偏心影响连接节点集中力变化区间较大,以下列出几种横梁连接方案供参考(图17、图18):
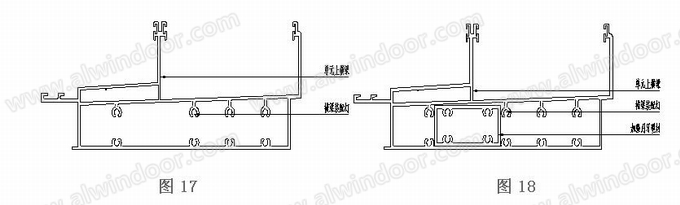
4、结语
现今建筑的外立面效果丰富多样,幕墙结构的受力也显现复杂化,本文通过对错缝式单元幕墙横梁连接设计剖析,总结一些体会与大家分享,希望给大家带来参考价值:
1、在错缝式幕墙设计初期应,整体性考虑错缝式效果,合理的布置错缝位置。
2、复杂受力体系分析时,尽量简化受力体系,并对计算数据结果进行验证。
参考文献
[1] 姚谏,董石麟.建筑结构静力计算实用手册.中国建筑工业出版社.2014
[2] 数字化手册编委会.机械设计手册.化学工业出版社.2008
作者单位:深圳市方大建科集团有限公司

