2.2.2 双跨梁力学参数的求解
对幕墙立柱进行结构分析计算时,需要计算的力学参数主要有:各支座反力、垂直于 轴方向的挠度、立柱
内力即弯矩和剪力等。下面给出其求解过程,假设立柱材料的
弹性模量为 ,其
截面对中性轴的
惯性矩为 。
我们知道,双跨梁的计算问题,实际上是一个超静定问题,因此必须要用到静力平衡条件和变形谐调条件。该问题的变形谐调条件就是在C支座处,垂直于 轴方向的挠度为0。
根据叠加原理,在小变形的前提下,在
弹性范围内,作用在立柱上的力是各自独立的,并不相互影响,各个荷载与它所引起的内力成线性关系,叠加各个荷载单独作用的内力,就可以得到共同作用时的内力。
因此为了计算分析更容易,我们可以对幕墙立柱的双跨梁力学模型进行简化,简化的思路是:先去除支座C,代之以支座反力 。于是双跨梁力学模型实际上可以当成下面两种简支梁力学模型的叠加,如图3和图4所示。
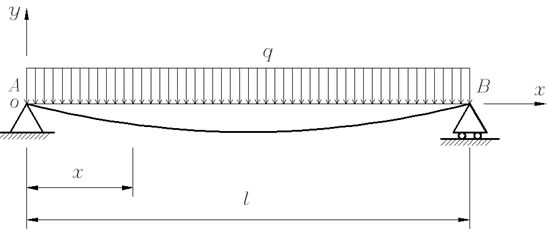
图3
图3表示的实际上就是双跨梁去除中间支座后的情况,是受呈线性分布的矩形荷载的简支梁,其荷载集度是 ,计算长度为 。设立柱中性层的挠度曲线为
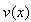
。
坐标为 的截面上的弯矩为
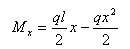
(1-1)
由于立柱中性层的挠度曲线方程为
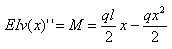
(1-2)
经两次积分得
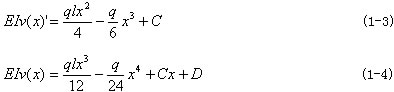
由于立柱在两端铰支座上的挠度都等于0,故得边界条件
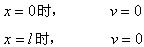
将以上边界条件代入(1-4)式,得
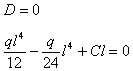
所以有
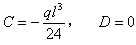
于是
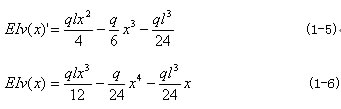
因为跨度中点挠度曲线的斜率为0,由此可以求得挠度的极值。
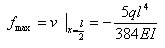
 上一页123456下一页
上一页123456下一页
