由表2可以看出双跨梁挠度的变化规律。当

=0.50时,相当于双跨梁的长、短跨相等,中间支座处挠度为0,各截面的挠度是以中间支座为中心对称分布的,这也与实际情况相符。当

=0.15时,短跨端支座处的挠度为0,随着立柱截面离短跨端支座距离
x增大,截面挠度逐渐增加,到一定值后,又逐渐减小,至中间支座处挠度又重新变为0;随着
x继续增加,挠度从0向相反方向增加(挠度系数是负,表示如图2所示变形情况下,挠度与
y轴正方向相反),到某个值后双开始变小,到长跨端支座处,挠度又重新变为0。其变化规律如图5所示。
进一步分析还可以得到三种挠度变化规律,均因

的变化而变化。当
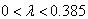
时,挠度f
x变化规律如图5所示;当

时,挠度f
x变化规律如图6所示;当

=0.50,挠度f
x变化规律如图7所示。

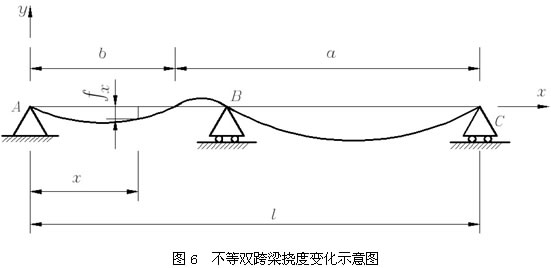
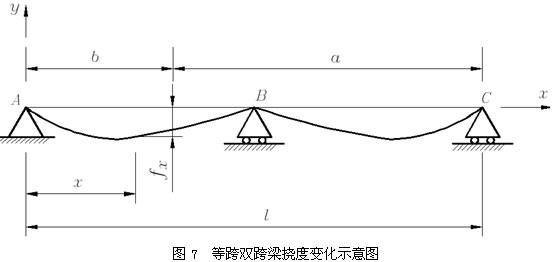
在工程实践中,幕墙立柱大多数情况下是在图5所示状态下工作,即

。
(3)

与最大弯矩
由式(1-15)和(1-16),并将式(1-12)、(1-13)和(1-14)的结果代入式中,化简可以得到坐标为
x的截面上的弯矩与

之间的关系。
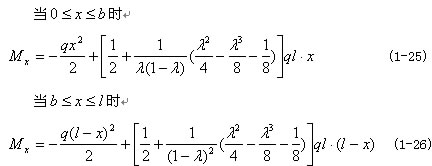
双跨梁的最大挠度出现在什么位置,同样与

有直接关系。

=0.10 、

=0.15 、

=0.40、

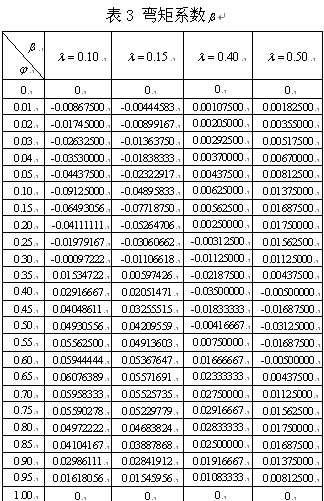
=0.50的情况为例,给出双跨梁不同截面的弯矩求解方法。如表3所示。截面位置以


 上一页123456下一页
上一页123456下一页
