2.2.3

与双跨梁的力学参数之间的关系
(1)

与支座反力
由式(1-12)、(1-13)和(1-14)可得如下表1:
表1 双跨梁支座反力系数表

因此有,
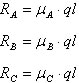
可见,双跨梁短跨端支座反力R
A是随着

从小变大在逐渐减小,并且其作用方向在改变。在如图2所示变形情况下,当

较小,R
A是负值,表示其方向向下,与荷载作用方向相同;中间支座反力R
C与长跨端支座反力R
B 为正,表示方向向上,与R
A方向和荷载作用方向相反。由表可知,当

>0.30后,R
A是开始转为正,表示其作用方向已经与R
C和R
B方向一致。
在对实际幕墙工程进行设计时,双跨梁短跨与全跨比例因子

不宜小于0.10,否则将使其中间支座反力R
C和短跨端支座反力R
A变得很大。如

=0.05时,中间支座反力 R
C=2.75658.
ql,是在同样外荷载作用下,简支梁端支座反力的5.5倍以上。
从表1还可以看出,最大支座反力总是出现在中间支座。因此,在进行幕墙设计时,如果采用双跨梁结构型式,按双跨梁力学模型进行计算分析,应该特别注意验算中间支座反力对结构的影响。如验算
预埋件和
连接件的
强度时,应该取中间支座反力为验算荷载。
(2)

与最大挠度
很显然,不等双跨梁最大挠度将产生在长跨范围内,所以可按式(1-20)来讨论 与最大挠度方间的关系。

其中

双跨梁的最大挠度出现在什么位置,与

有直接关系。下面以

=0.10 、

=0.15 、

=0.40、

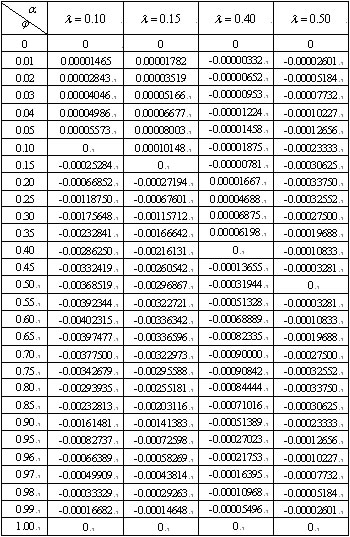
=0.50的情况为例,给出双跨梁不同截面的挠度值求解方法。如表2所示。

表2 挠度系数a
 上一页123456下一页
上一页123456下一页
